前面在介紹 Entropy（熵） 的時候，我們提到它可以用來衡量資料的不確定性和驚喜程度，而在 Decision Tree 裡，我們利用 entropy 來判斷資料的純度或是不確定性。

延續這個概念，當我們在訓練分類模型時，我們需要一個能夠衡量預測結果與正確答案差異的指標。

除了常見的「準確率（Accuracy）」之外， Cross-Entropy（交叉熵） 是更常用、也更敏感的一個損失函數（loss function），它能夠幫助模型在訓練過程中更精確地學習。

以下就來談談 Cross-entropy～

Cross-Entropy

• Entropy表示的是不確定性以及驚喜的程度
• Cross-entropy又可以叫做log loss，是最常用來衡量、改善機器學習、分類模型表現的損失函數（loss function）

以下為cross-entropy loss function的示意圖：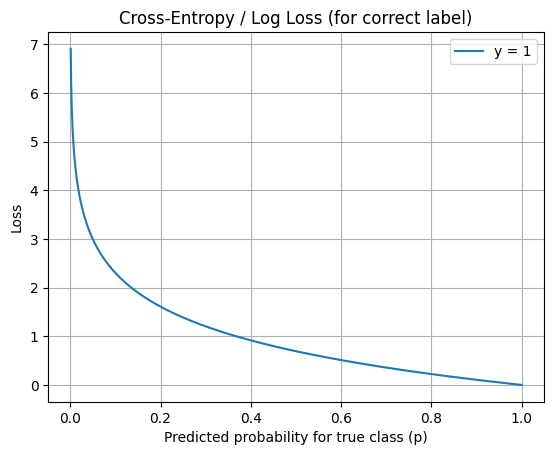

• 從上圖曲線可以看出，當預測機率越大時，log loss就會越小，但是預測機率越小，log loss就會增加得很快。
• 簡單來說，cross-entropy就是在計算真實機率分布，以及預測值之間的差異
• 值越小代表模型表現越好，而我們就可以利用cross-entropy來調整權重（weights），進而改善模型的表現

Cross-entropy vs. KL Divergence

KL Divergence也是在比較兩種機率之間的差異，兩者之間有什麼差異呢？

➔ KL divergence是在計算真實機率以及近似它的機率之間的差異，但是cross-entropy是在計算模型產出機率分布到真實機率之間的距離

假設有一個二元（binary）分類任務

以下為binary cross-entropy公式（針對所有資料）：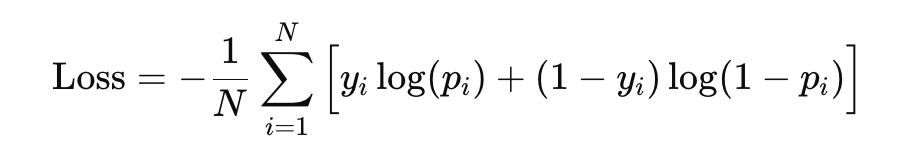

• N：資料筆數
• yi：第 i 筆資料的真實標籤（0 或 1）
• pi：模型預測該資料屬於「1 類別」的機率
• log⁡：通常是自然對數（ln）

若是只要單看一個資料的損失，以下為公式（假設正確值為1）：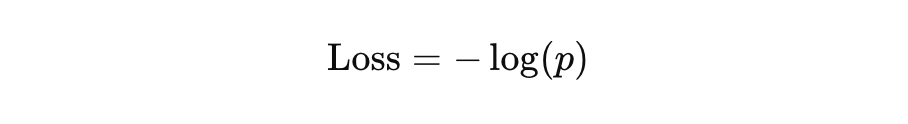

那麼為何不用模型的錯誤率來去看模型的表現度呢？

• 兩個模型可能錯誤率一樣，但實際上模型的預測「信心程度」可能差很多。
• 錯誤率只告訴我們預測對或錯，無法反映模型真實學習到資料的準確程度。
• 舉例來說：

假設學生 A 和學生 B 都考了 90 分。
B 是靠實力答對所有題目，而 A 有一半題目是靠猜中得分。
從分數上看，兩人一樣，但實際學習成效卻不同。

Cross-Entropy就像考慮學生「答題信心」的指標，能反映模型的實際表現，而不只是對錯。

Reference 1
Reference 2
Reference 3